Matematické funkce
Funkce se zapisuje ve tvaru f: y=f(x). Funkci můžeme popsat analyticky (rovnicí), grafem, tabulkou nebo slovním popisem. Pro funkci existují jistá pravidla. Je tedy třeba nejdříve rozlišit zda-li se vůbec jedná o funkci.
Funkce je předpis, který každému x množiny M přiřadí právě jedno y z množiny N.
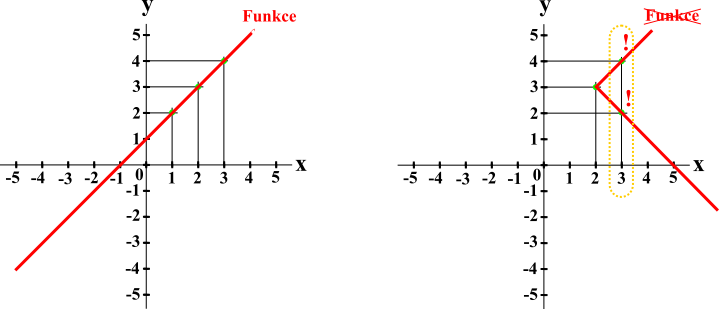
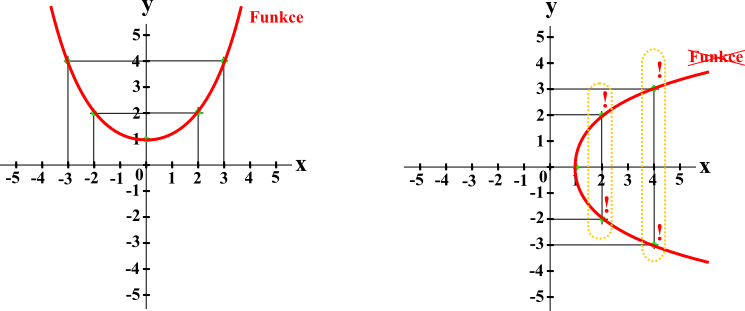
Na ose x nemůžeme tedy vytyčit ve stejném místě dva a více bodů y (podobně jako v jeden časový okamžik nemůžeme být na dvou místech). Hodnota x v daném místě grafu může mít pouze jednu hodnotu y. V opačném případě se nejedná o funkci.
Hodnota y může však být stejná pro vícero hodnot x (podobně jako jedno místo můžeme navštívit něklikrát v různém čase, za den).

Definiční obor funkce se značí D(f). Udává jakých čísel, hodnot argumentu x může funkce v celém svém průběhu nabývat. Např. pro f: y=x je D(f) = R (x můžou být všechna reálná číla). Pro f: y=1/x však honota x nemůže být nula (nelze dělit nulou), definiční oboru bude tedy D(f)=R-{0} (všechna reálná čísla kromě čísla 0). Definiční obor tedy udává, jaká čísla lze dosadit za x, aby vyšel výsledek funkce.
Obor hodnot funkce se značí H(f). Udává jakých čísel, hodnot může nabývat argument y po dosažení jakéhokoliv x z definičního oboru.
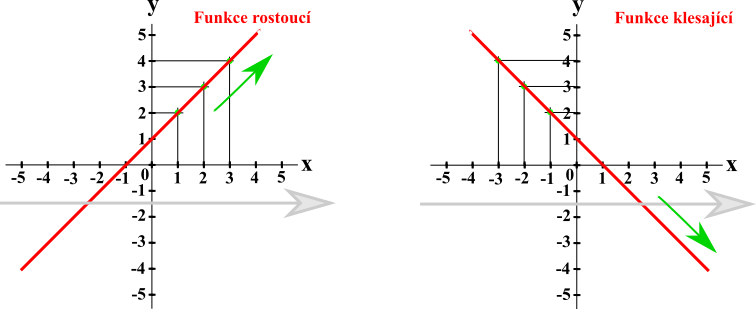
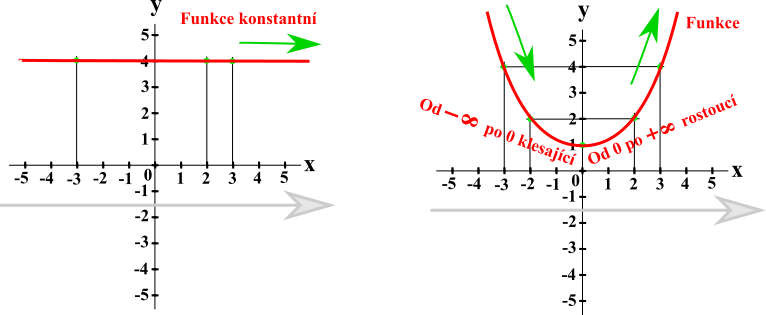
Monotónost funkce určuje, zda-li je funkce v daném úseku nebo v celém svém průběhu rostoucí, klesající nebo konstantní.
Konstantní funkce: x1 ≠ x2 ⇒ f(x1) = f(x2)Rostoucí funkce: x1 < x2 ⇒ f(x1) < f(x2)
Klesající funkce: x1 < x2 ⇒ f(x1) > f(x2)

Prostá funkce je taková, pro kterou platí v celém jejím průběhu pro každé y pouze jedno x.

Parita funkce popisuje souměrnost funkce. Sudá funkce je souměrná dle osy y. Lichá funkce je souměrná podle počátku.
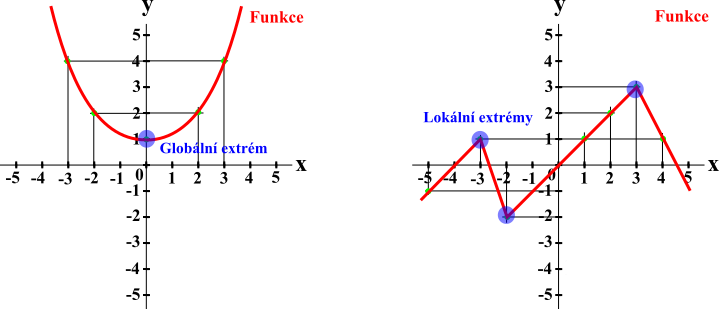
Extrémy jsou maxima a minima funkce. Globální extrém je např. minimální nebo maximální hodnota celého průběhu funkce dle D(f). Lokální extrémy jsou lokální maxima a minima v průběhu vymezeného úseku funkce.
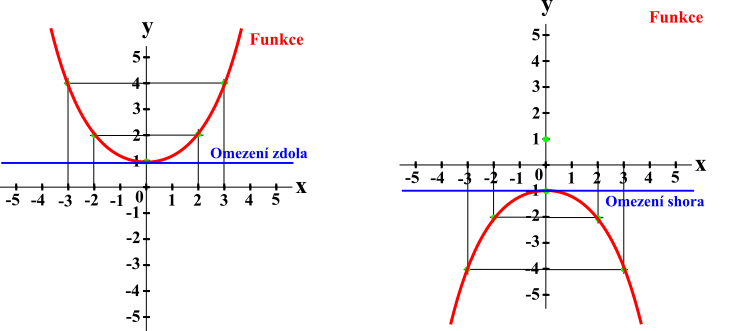

Omezenost funkce je minimální nebo maximální hodnota y dle H(f), které může funkce dosáhnout. Funkce může být omezená zdola, shora, zdola a shora, může být také pokračující oběma směry do nekonečna a tak bez omezení.
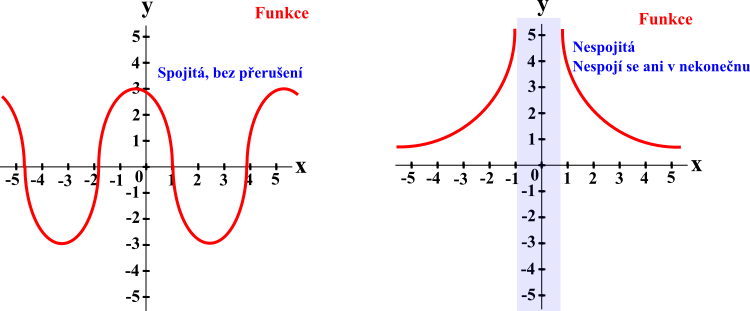
Spojitost funkce určuje možné přerušení spojitého, spojeného prúběhu. Pokud je funkce bez přerušení v celém D(f), pak je spojitá. Pokud má funkce přerušení, pak je nespojitá.
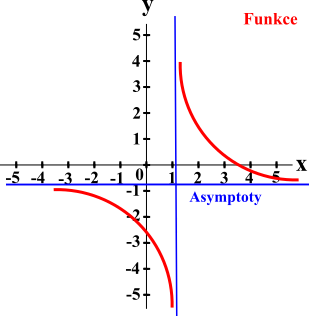
Asymptoty jsou přímky, kterým se nespojitá funkce přibližuje. Graf funkce nikdy tyto přímky neprotne ani v nekonečnu.

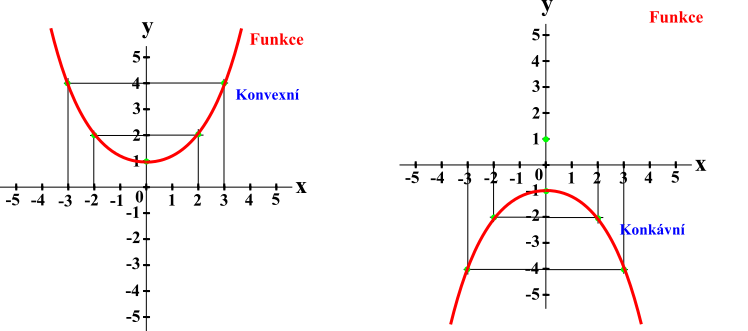
Funkce může být konvexní (tvar U) s omezením zdola, nebo konkávní (tvar ∩) s omezením shora.
U složitější funkce může být konvexní nebo konkávní jen část grafu funkce. Inflexní body určují místa, kde se mění graf z konvexního na konkávní či naopak.
